a) (12x² - 8x) : (2x)

b) (x² + 5x +6) : (x + 2)

c) (x² - 7x + 10) : (x - 2)

Espero que tenham entendido!!
Bjss*
Projeto realizado pela profª Thamires do colégio Miguel Couto. Welcome to our blog!



 3x² + 5x + 9 e Q(x)
3x² + 5x + 9 e Q(x)  ax² + bx + c. Dizemos que P(x) é idêndico a Q(x) se, e somente se, P(α) = Q(α) para qualquer α
ax² + bx + c. Dizemos que P(x) é idêndico a Q(x) se, e somente se, P(α) = Q(α) para qualquer α 
 . Desse modo, atribuindo valores a x, podemos determinar os coeficientes a, b e c para que os polinômios sejam idênticos.
. Desse modo, atribuindo valores a x, podemos determinar os coeficientes a, b e c para que os polinômios sejam idênticos. 
 e
e  , na variável x, são idênticos se, e somente se:
, na variável x, são idênticos se, e somente se: com
com  |N e 0
|N e 0  j
j  n
n Q(x); caso não sejam idênticos, indicamos por P(x)
Q(x); caso não sejam idênticos, indicamos por P(x)  Q(x).
Q(x).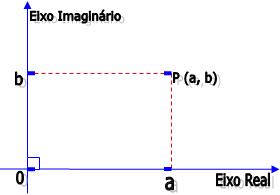

|
|
.jpg)
.jpg)
.jpg)
.jpg)
.jpg)
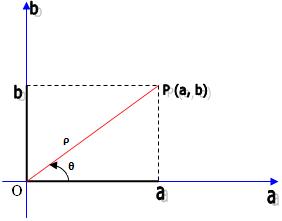
 , que podem ser escritos na forma algébrica, que seria: z = a +bi com {a,b} onde a e b são números reais e i denota a unidade imaginária.
, que podem ser escritos na forma algébrica, que seria: z = a +bi com {a,b} onde a e b são números reais e i denota a unidade imaginária.